前面講了一些基本的傳遞函數，但是這些都是開環電路的傳遞函數，我們現在來闡述一下基本的閉環系統的傳遞函數。

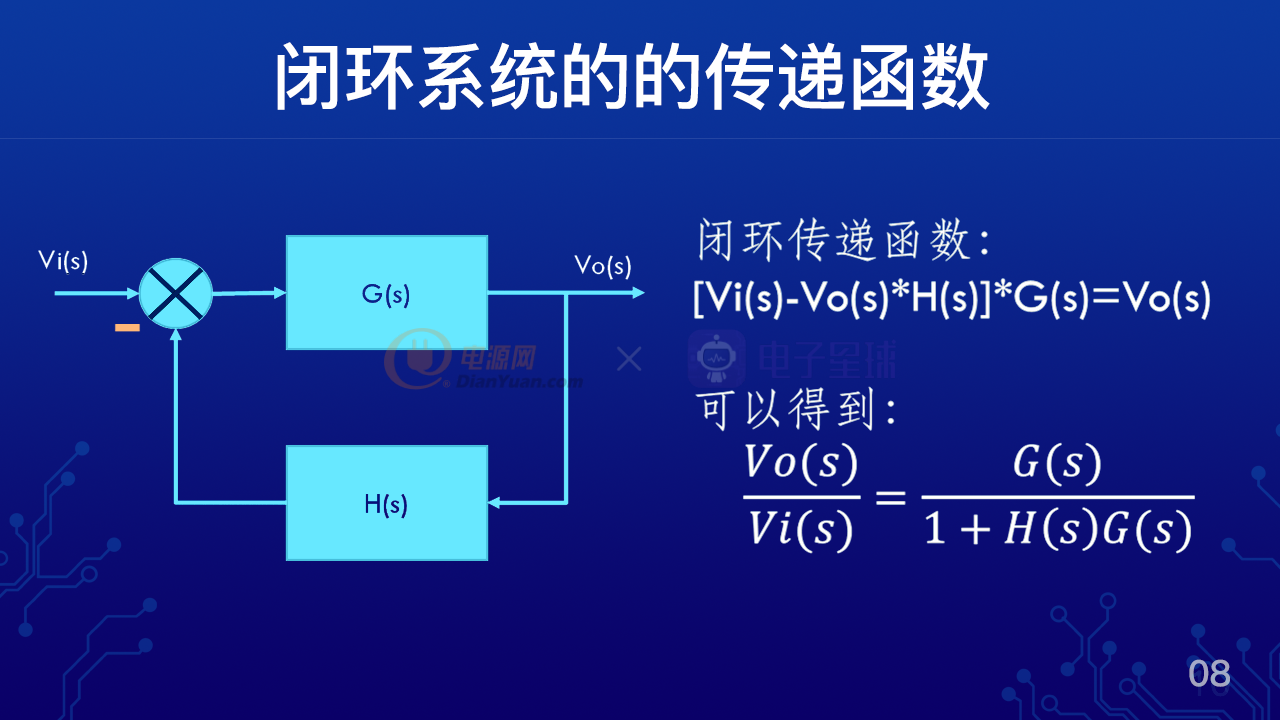
左邊框圖表示了一個帶有負反饋的閉環系統，其中Vi（s）為輸入信號，Vo（s）為輸出信號，G（s）為前項的傳遞函數，H（s）反饋傳遞函數，那么我們就可以得到這樣一個等式，[Vi（s）-Vo（s）*H（s）]*G（s）=Vo（s），這里的Vo（s）*H（s）為反饋過來的信號，那么把這個等式經過變化之后就可以得到Vo（s）/Vi（s）= G（s）/[1+H（s）G（s）]，這樣的表達方式我們稱之為標準的閉環傳遞函數。其中H（s）*G（s）為開環傳遞函數，那么這樣的閉環傳遞函數表達了輸出Vo和輸入Vi的一種關系函數。

從閉環傳遞函數，我們同時可以得到一個線索，如果H（s）*G（s）也就是開環傳遞函數，正好等于-1的時候，那么 Vo/Vi就會變得無窮大，也就是說這個時候系統會產生自激震蕩，那么在復數里面-1表示什么呢？它表示的就是增益為1，或者說0db相位180度。由此我們可以得出什么結論呢？在這樣一個負反饋系統里面，如果開環傳遞函數的增益等于0，或者說0db，同時相移為180度的時候，整個系統就會出現自激震蕩。所以我們在設計閉環反饋系統的時候，要避免出現這樣的情況。

那么這里要強調一點，有的時候我們會把負的H（s）乘以G（s）嘴開環傳遞函數，也就是說把反饋里面的減號算在開環傳遞函數里面，如果這樣的話，計算出來的結果要在開環傳遞函數等于1的時候，系統會產生自激震蕩。那么傳遞函數等于1，就表示著增益為0db，相移為360度。事實上我們在計算電源補償環節的時候，經常有人會搞錯負號的計算，導致兩種計算的相位相差了180度。

剛才我們說到可以根據開環的傳遞函數來判斷什么時候會產生自激震蕩。為了避免這種自激震蕩，我們就需要避免開環傳遞函數等于-1的情況，意味著不能讓增益等于0db，相位等于180度，這兩種條件同時出現，這樣才能保證系統的穩定性。

那么我們怎么來判斷反饋系統有足夠的穩定性呢？有一種非常簡單的辦法，就是描繪波特圖來判定。

如何描繪波特圖呢？ 首先我們要把開環傳遞函數就是H（s）乘以G（s）的函數公式寫出來，這個公式寫出來之后一定是一個復數函數，然后對這個復數函數求模，把求出來的模以橫軸為頻率，縱軸為增益的形式描繪出來。其次，可以對負數函數求角度，也就是相位，把相位以同樣的方式描繪出來，這樣就形成了開放函數的波特圖。

波特圖里面包含了增益曲線和相位曲線，那么如圖中所示，圖中的藍色曲線為增益曲線，紅色曲線為相位曲線，從這個波特圖中我們就可以得到三個重要的參數。

第一個就是相位余量。什么是相位余量？就是當增益穿過0db的時候，相位離180度還有多少余量。這里還要強調一下，如果開環傳遞函數是負的H（s）乘以G（s）那么就是離360度或者0度還有多少余量稱為相位余量。通常我們認為相位余量大于45度，是足夠維持系統穩定性的。

第二個就是增益余量。當開環傳遞函數相位達到180度或者0度的時候，增益離0db的余量叫做增益余量。我們認為小于-6db就可以維持系統穩定。

這兩個余量都是為了避免系統產生自激震蕩而保留的余量。但是在很多情況下，有些客戶會要求我們設計的電源系統相位余量達到60度，增益余量達到-10db，這些更高的要求。

第三個參數就是帶寬或者說穿越頻率，在開關電源系統里面，我們希望帶寬越寬越好，帶寬寬意味著動態響應更容易做好，但實際上電源系統的帶寬是受到約束的。一般情況下，電源的帶寬受開關頻率的限制，通常我們會把帶寬設計在1/5~1/6開關頻率以下，但是如果這個電源系統有右半平面零點，那么帶寬就會設置在1/3右半平面零點以下。

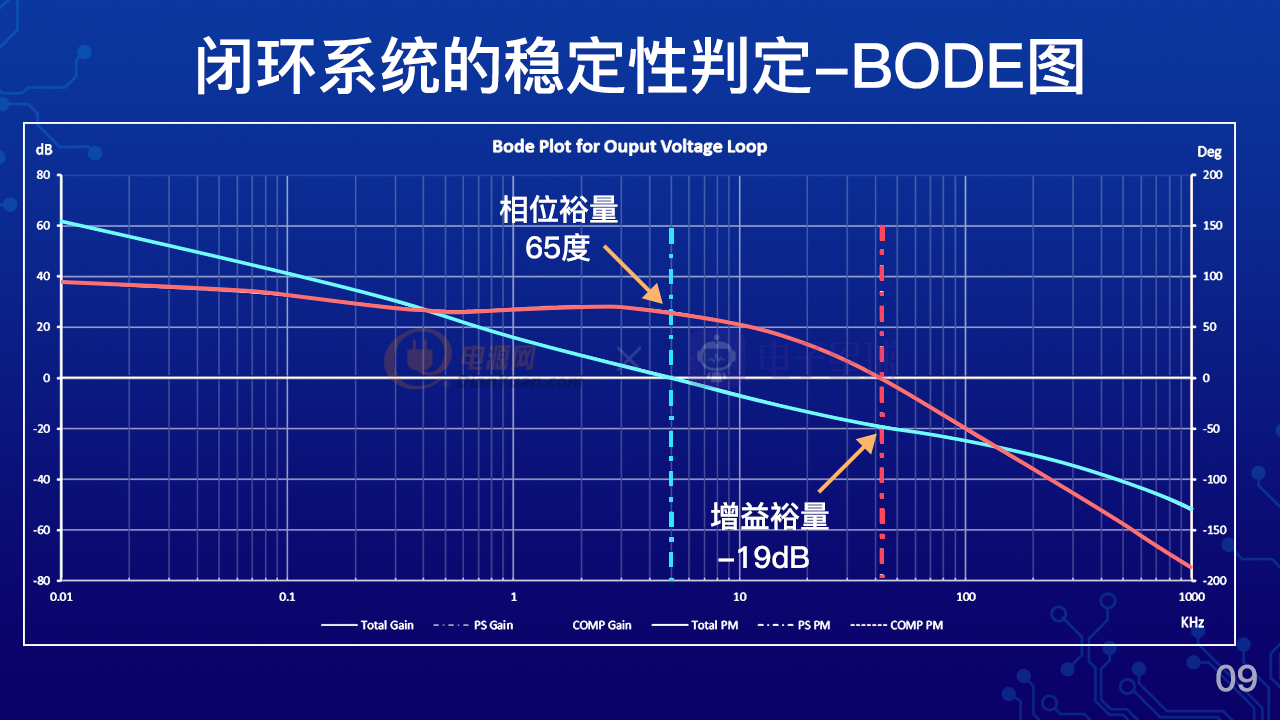
在這張圖里面我們可以看到這個波特圖的相位余量為65度，增益余量為-19db，而帶寬大概在5k左右，在我們實際設計中不可能把三個參數都設置的最優，因為他們都有互相牽制的作用，所以這三個參數一定是全盤考慮折中之后的結果。

在開關電源系統里面，我們通常把整個開關函數分成兩個大的環節，比如圖中所示的電壓型buck電路，我們把紅框里面的電路做一個環節，這個環節所表達的函數F（s）=d（s）/Vo（s），這個表達式的物理意義就是當Vo產生變化的時候，占空比會怎么變化。籃筐里面的電路作為另外一個環節，那就是P（s）=Vo（s）/d（s），它表達了當占空比變化的時候，Vo又會怎樣變化。那么F（s）乘以P（s）就形成了該電源的開環傳遞函數。

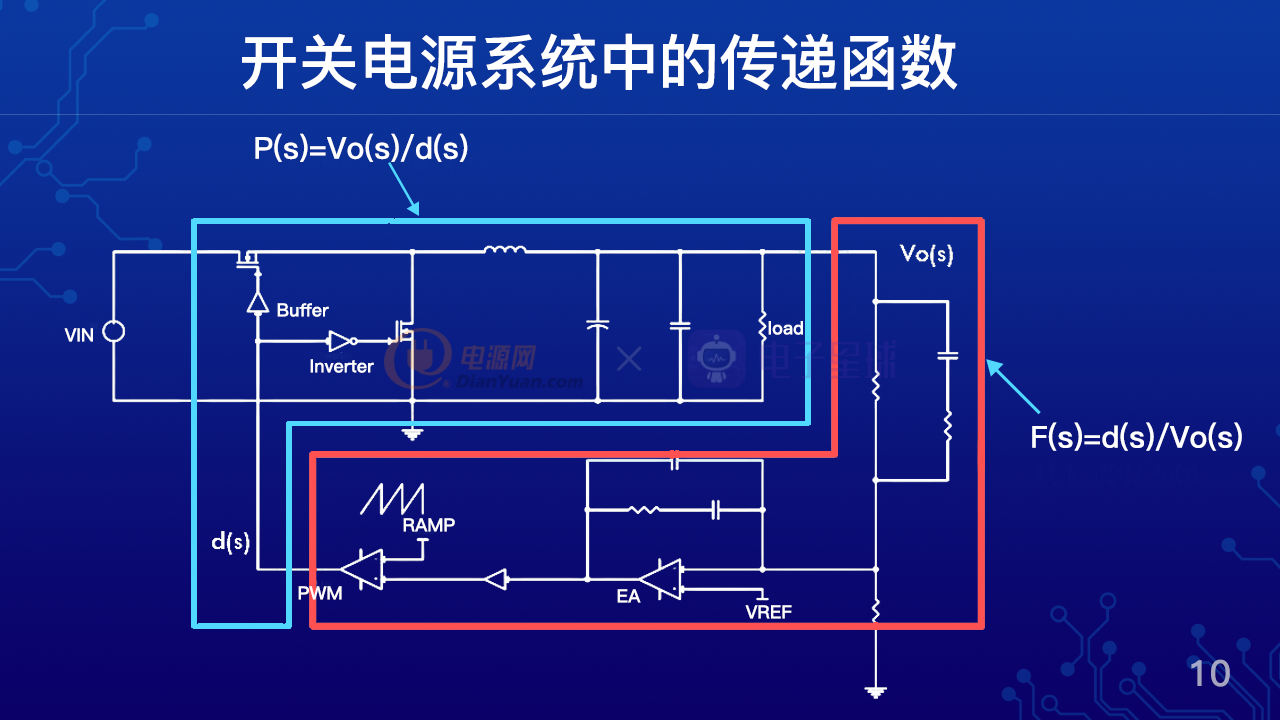
接下來我們就要去做的就是，第一步，把F（s）和P（s）的傳遞函數寫出來，然后把兩個函數相乘，最后形成一個總的開環傳遞函數。第二步，把這總的開環傳遞函數的模和相位求出來，并且以波特圖的形式把曲線描繪出來。第三步，根據波特圖來判斷其穩定性。

我們可以說第一步是最關鍵的一步，也是最難的一步，我們來看一下電路圖，為什么我們要把它分成兩個環節。一個是紅框里面的電路，一個是籃筐里面的電路。因為我們可以看到紅框里面的電路是完全線性的電路，對線性電路來說，我們只要學過電路原理，都能輕松的寫出傳遞函數。但是籃筐里面電路卻是包含了開關電路，這是個非常典型的非線性電路，對于非線性電路理論上是寫不出傳遞函數的。

這里來介紹一下什么是線性電路呢？就是全由線性元器件組成的電路稱之為線性電路。比方說我們常用的電阻，電容和電感，以及運算放大器等就是線性元件，因為他們的參數并不會隨著外界條件的改變而改變。比方說電感的感量，理論上是不會隨著電感電流變化，又比如說電容的容量也不會隨著電容上的電壓變化，這樣的元器件稱之為線性元件。但是什么又是非線性元件呢？比如mos管，mos管工作在開關狀態的時候，它是受門極電壓控制的，當門極電壓是高電平的時候，導通mos管可以等效為一個很小的電阻，但是當門極電壓是低電平時，mos管關斷，它又可以等效為開路模式。就是這種參數受其他條件控制的元器件稱之為非線性器件，包含了非線性器件的電路，就是非線性電路。

當然我們實際應用的電感和電容多多少少有點非線性特性，比如電感的感量實際上會隨著電感電流增大而下降，而某些電容的容值也會隨著電容上的電壓增大而減小。但是我們在理論分析的時候，還是會把這些元器件當做線性元件來分析。

早在上個世紀開關電源的穩定性分析一直困擾著電源工程師，因為大家都知道開關電源是非線性系統，無法寫出線性電路中的傳遞函數，而非線性電路理論又是大家不熟悉的知識，所以基本上電源的穩定性只能靠測試、經驗等方式來解決，直到幾位美國的大學教授開辟了一個新的路徑，就是把非線性電路線性化，我們現在常說的狀態空間平均法。狀態空間平均法的要義就是把離散的周期信號平均化，然后近似為連續信號。

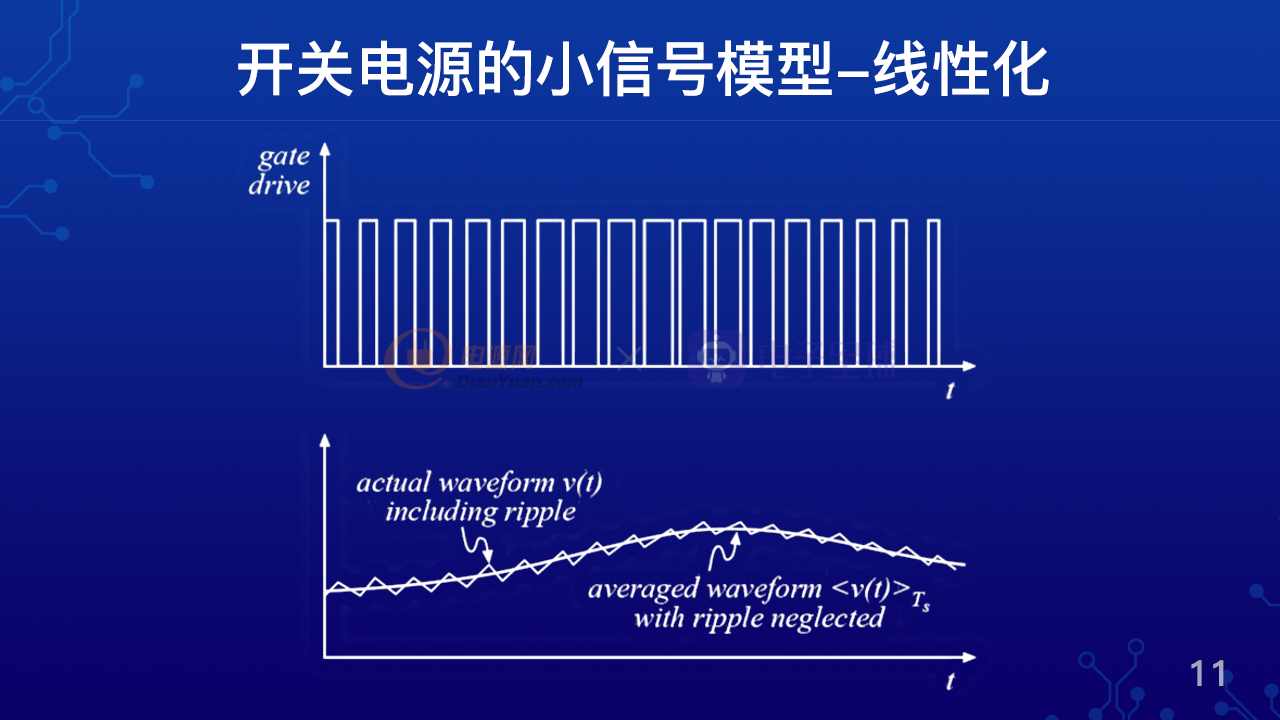
比如上圖的脈沖波，為一串占空比不斷變化的脈沖，這就是一個離散的信號。如果我們把這些信號在一個周期內做平均，或者說我們來個低通濾波器，濾掉高頻信號，我們就可以得到一個帶有開關紋波的連續波動信號。再次把開關頻率的紋波抹掉，我們就可以得到一個連續光滑的波動曲線。這樣我們就把脈沖電壓信號平均等效為下圖中的連續信號。基于這樣的思路，就可以把開關電源中的一些周期開關信號平均為連續信號，并且把開關電路等效為一些線性電路。

基于這種近似等效的方法，我們就可以建立開關電源的交流小信號模型。為什么叫交流小信號模型呢？因為這種模型是建立在直流工作點上的交流模型，而且這個模型只有在傳遞足夠小的信號前提下，才能保證準確性，但是這種模型對開關電源的環路分析具有非常重大的意義。這種模型由于做了平均化，事實上只有在低頻信號下才是準確的。如果當信號頻率開始接近脈沖信號頻率的時候，它的準確度就會大大降低。比如下圖中的連續信號，包含了低頻的勞動和脈沖頻率的波動，平均法建立的模型對低頻勞動來說是準確的，但是對脈沖頻率的勞動是不準確的。

在我們實際應用中，通常認為信號頻率低于開關頻率的1/3，可以認為是比較準確的，低于開關頻率的1/10，這種模型可以認為是非常準確。那么這個狀態空間平均法雖然是采用了近似的方式把開關電路線性化了，有著很多的局限性，可是他的理論簡單易懂，方法直接有效。所以到目前為止，依然是最受歡迎的分析方法。

雖然利用狀態空間平均法推導小信號模型，在學術上被認為是相對簡單的方法，但是實際上它并沒有那么簡單，還是需要繁瑣的公式推導，這就需要相當的數學功底。雖然這些知識在我們一些大學教科書上已經被詳細的闡述了，但是很多工程師還是無法準確地推導出小信號模型。不過幸好我們電源所用的大多數拓撲都是被研究了一次又一次，所以基本上常見的拓撲小信號模型都已經被推導過了，我們只要直接拿來用就可以了。

這里我們就來看一下三個基本拓撲Buck、Boost、Buck-Boost。

在電壓模式下的小信號模型，這邊采用一個統一的公式來表達三個拓撲的小信號模型， 那就是：

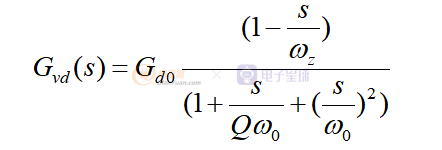
在這Gvd（s）表達了 V o的變化除以占空比的變化。也就是說當占空比在某個直流工作點的基礎上，出現了正弦波的交流勞動，那么這個勞動最后會傳遞到輸出，這個傳遞函數就是表達了輸出和占空比之間的關系。

仔細看一下這個傳遞函數它包含了三個要素，首先是直流增益Gd0，還有是一個右半平面零點ωz和一對復合雙極點ω0。

具體來先看Buck電路，Buck電路的直流增益為V/D，其中的V表示為輸出電壓，那么V/D實際上就是輸入電壓，所以我們可以說Buck電路的直流增益就是輸入電壓。其次為復合雙極點的位置，這個雙極點的位置在：

這里的R為負載電阻，那么理論上來說當空載的時候，也就是R為無窮大的時候，Q值應該也是無窮大。但是我們實際在測試的時候，即便是空載Buck電路的Q值也沒有那么的大，那是因為在實際中電感的直流電阻，mos管的導通電阻都會降低Q值，只不過在理論分析的時候沒有把它們考慮進去。

最后一個參數就是右半平面零點ωz，事實上Buck電路是沒有右半平面零點的，所以這里就是無窮大。

表的下面兩行同樣列出了Boost和Buck-Boost 4個參數，最主要的不同是Buck沒有右半平面零點，而Boost和Buck-Boost有零點。

我們前面也講了，右半平面零點是無法補償的，所以Boost和Buck-Boost的環路帶寬必須低于右半平面零點。而在實際上為了可靠性，一般會把帶寬設計在低于1/3的右半平面零點。如果以Boost為例，我們可以看到占空比越大，負載越重，電感越大，那么右半平面零點的頻率越低，所以在設計Boost的時候，為了避免右半平面零點頻率過低，電感量必須盡量取小。

當然這里的模型是在連續模式下推導出來的，如果是在DCM也就是在斷續模式下傳遞函數就會有很大的不同。最大的變化就是Boost和Buck-Boost的右半平面零點就不存在了。

除了電壓型控制之外，最受歡迎的控制方式就是電流型控制。電流型控制里面比較常用的是峰值電流和谷底電流控制。和電壓型不同的是電流型控制常規模型里面并沒有lc形成的復合雙極點，取而代之的是兩個分開的極點，一個在低頻處，另外一個在高頻處。因為一般情況下高頻極點遠遠高于環路帶寬，所以可以忽略掉。為了簡化計算，我們只有可以用一個一階系統的傳遞函數來表達電流型控制，那么它表達公式為：

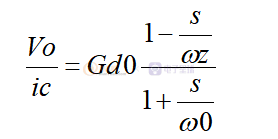
這里的ic表示為受控電流，也就是電感電流的勞動。這個傳遞函數表達了什么呢？當電感電流出現擾動，最后傳遞到輸出電壓的勞動是什么樣的。

和電壓模式一樣，它也包含了三個基本參數，一個就是直流增益Gd0，一個就是右半平面零點ωz，另外就是一個單極點ω0。

以Boost為例，我們可以看到直流增益Gd0為：

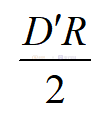
這里的D'=1-D。那么單極點的位置為2/RC，右半平面零點的位置依然為和電壓型控制一樣為：

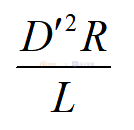
我們可以看到這個傳遞函數里面只有一個極點，但是在實際應用的時候，電流型控制通常是要加斜率補償，加了斜率補償之后，高頻極點的位置就會往低頻段挪，那樣有時候我們就不能忽略掉這個極點，這個時候我們就需要更為精確的數學模型，如果大家對更為精確的數學模型感興趣的話，可以參考一些文獻，甚至有些文獻推導出來具有三個起點的精確模型。

那么最后這里再強調一下，對于Boost和Buck-Boost電流型控制并不能消除它們的右半平面零點。

剛才的小信號模型為了簡化公式推導，都沒有考慮輸出電容的ESR，但是在實際應用中，電容或多或少存在ESR，特別是電解電容的ESR更不能忽視。所以我們在計算模型的時候還是要把ESR考慮進去。這里來講一下電容ESR對環路帶來的影響。

首先如果輸出只有一個電容，那么電容的ESR會給環路帶來一個零點，零點的位置就是ωz=1/RC，或者說 Sz=2π*1/RC，這里的R就是電容ESR。

但是如果有多個電容并聯，那么多個電容并聯會給我們計算帶來很大的麻煩。很多人喜歡把多個電容等效為一個電容，但實際上只有多個相同的電容才能等效為一個電容，如果多個不同的電容并聯，不能簡單的等效。

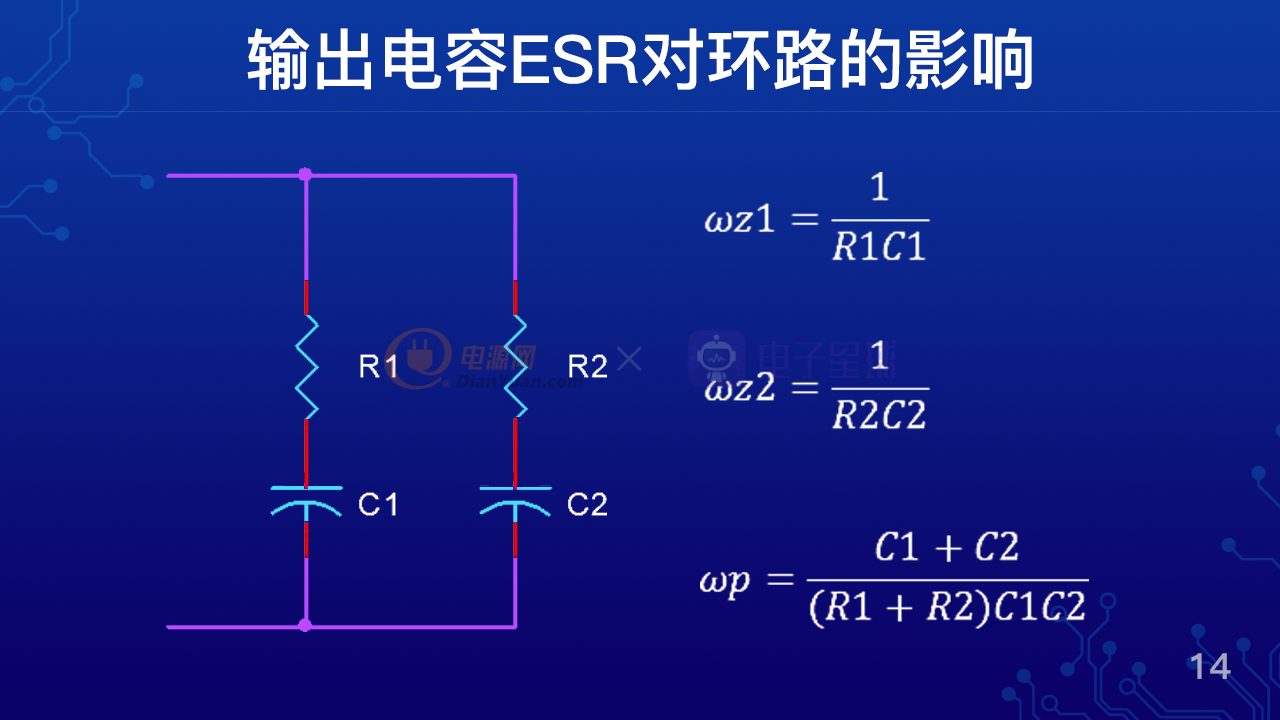
我們來看一下一個兩個電容并聯的例子，C1和C2并聯分別有兩個ESR，R1和R2。那么我們可以推導出實際上兩個電容并聯會給環路帶來兩個零點和一個極點，分別是ωz1=1/R1C1，ωz2=1/R2C2，ωp=（C1+C2）/（R1+R2）C1C2。這里ωz1和ωz2是兩個零點，ωp是一個極點。那么我們可以看出來，只有當C1=C2的時候，并且R1也等于R2的時候，那么其中一個零點就可以把極點抵消掉，這樣的話我們就才可以等效為一個電容，可以認為它帶來了一個零點。

如果是更多不同的電容并聯，那么情況會變得更復雜。所以有時候電容也是我們實際情況和理論有所差異的一個重要原因。