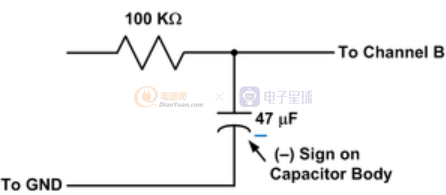
電容器由兩個導體組成，通常稱為“極板”，由稱為“電介質”的絕緣材料隔開。在電路中，電容器的使用方式是在每個板上產生相等和相反的電荷。電荷是由導體中自由電子的積累或耗盡產生的。電荷在電介質中產生電場，從而在極板上產生電壓。對于板上的固定電荷 Q，板上的電壓V由電容值 C 根據以下關系確定。

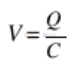
如果我們想確定電壓和電流之間的關系，重新排列方程如下是有用的。

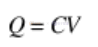
由于電流是 Q 的時間導數，因此取每一邊的一階時間導數 - 注意 C 是常數 - 會產生一個表達式，將電流與電容器中電壓的變化率聯系起來。

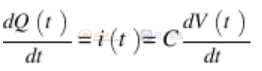
這可以明確地寫成電壓變化率。

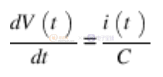
我們可以使用這個方程來研究電容器的充電。如果我們有一個恒流源 I，電容器將以每秒 I/C 伏特的恒定速率充電。在 RC 電路中，我們有一個與電阻串聯的電壓源，而不是電流源。當 5 V最初應用于電路時，它都出現在電阻器上，因為電容器上的初始零電壓不能立即改變（當然，除非我們有無限電流可用）。在第一個電路中，電阻兩端的 5V 根據歐姆定律產生 5V/100K 安培的電流，開始為電容器充電。然而，當電容器充電時，電阻兩端的電壓會按照基爾霍夫電壓定律下降，從而降低電流和電容器電壓的變化率。該過程使電容器電壓的增加速度呈指數減慢。

RC 電路中的充電速率取決于 RC 乘積，通常稱為“時間常數”，由希臘字母 tau 表示。在一個時間常數內，充電電容器將從其當前電壓移動 63% 到通過電阻器施加的電壓。施加階躍電壓V T的 RC 電路中的電容器電壓V C由以下等式控制。

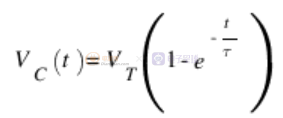
在一個時間常數中，電容器達到施加電壓的大約 63%，在五個時間常數中達到大約施加電壓的 99.3%。從實際角度來看，電容器充滿電所需的時間通常被視為五個時間常數。在第一個電路中，時間常數為 (100 KΩ)*(47 μF) = 4.7 秒，使電容器充滿電的時間約為 23.5 秒。充電和放電的時間常數相同，因此當通道 A 的電壓降至零伏時，電容器完全放電大約需要 23.5 秒。