前言:定點(diǎn)是個(gè)好東西,就是編碼有點(diǎn)難受。但是找到了一些定點(diǎn)編程的方法后,我們還是能理解它,掌握它,運(yùn)用它。畢竟浮點(diǎn)的單片機(jī)很貴,定點(diǎn)的單片機(jī)很便宜。作者上手第一個(gè)單片機(jī)就是支持浮點(diǎn)的,編碼的思想一直都是浮點(diǎn),管你3721直接干就完了。但是最近因?yàn)樾枰鲆恍┒c(diǎn)的功能開發(fā),就被迫去學(xué)習(xí)一些關(guān)于定點(diǎn)的實(shí)現(xiàn)了。
定點(diǎn)計(jì)算的幾個(gè)基本點(diǎn):
-
IQ格式的定點(diǎn)相乘等于Q相加,除法就是減少
-
相同IQ格式的定點(diǎn)可以直接加減
-
可以利用移位來(lái)實(shí)現(xiàn)數(shù)字放大或縮小
定點(diǎn)的目是將浮點(diǎn)數(shù)字放大X倍來(lái)抵消整數(shù)計(jì)算時(shí)丟失的數(shù)字誤差,比如0.0001f轉(zhuǎn)為定點(diǎn)數(shù)字就是直接將浮點(diǎn)數(shù)字乘以2^X這個(gè)數(shù)字,如果IQ轉(zhuǎn)換數(shù)字足夠大,就可以減弱整數(shù)數(shù)值計(jì)算的誤差。根據(jù)IEE754標(biāo)準(zhǔn)的單精度浮點(diǎn)數(shù),小數(shù)點(diǎn)后的浮點(diǎn)數(shù)字編碼最大利用到24位,因此理論上使用IQ24的定點(diǎn)數(shù)(#define _IQ24(A) (long) ((A) * 16777216.0L))就可以等于浮點(diǎn)的小數(shù)點(diǎn)誤差。TI的IQMATH庫(kù)函數(shù)默認(rèn)使用IQ24的格式就是因?yàn)檫@個(gè)原因。
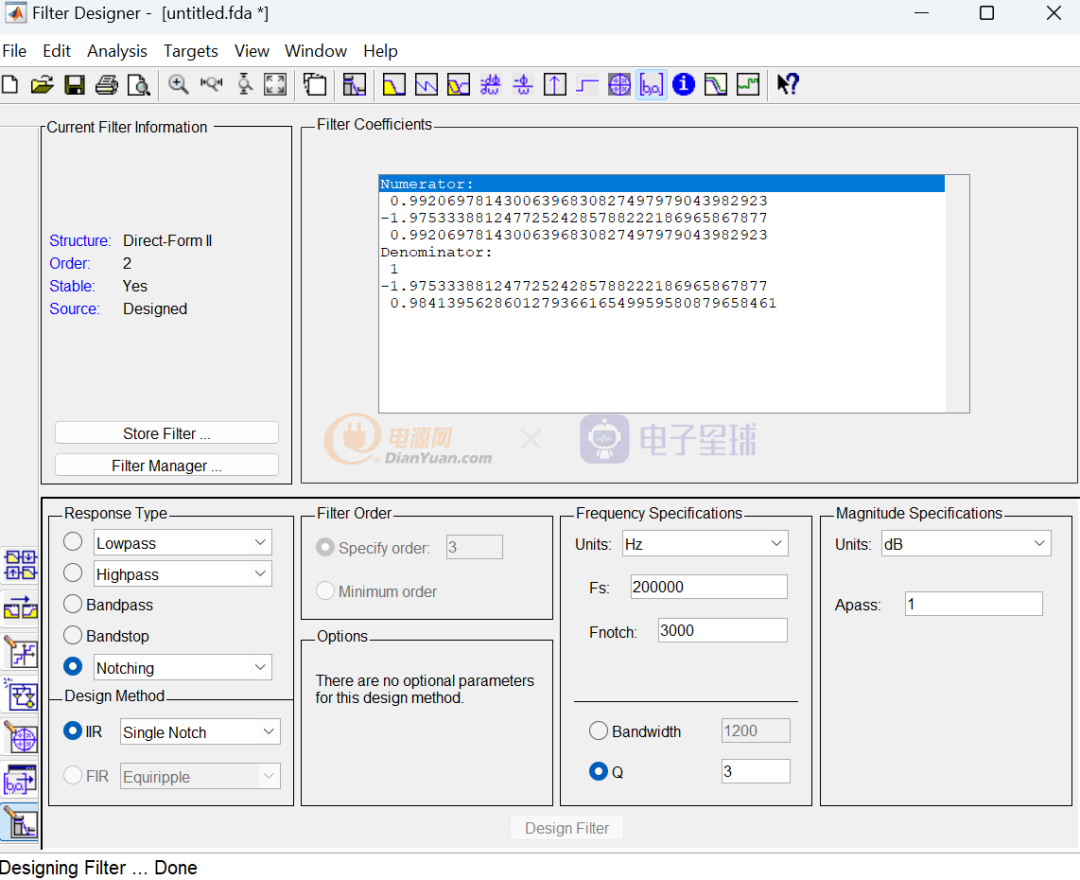
利用這一點(diǎn)可以使用定點(diǎn)計(jì)算來(lái)獲得比單精度浮點(diǎn)更高的算法,比如高階的濾波器設(shè)計(jì)中,時(shí)常因?yàn)椴蓸宇l率非常高導(dǎo)致離散化之后離散傳遞函數(shù)中多項(xiàng)式中的系數(shù)很小,因?yàn)楦↑c(diǎn)數(shù)量化誤差導(dǎo)致的濾波器誤差。筆者之前就有遇到一個(gè)帶通濾波器因?yàn)榱炕`差的問(wèn)題,導(dǎo)致一直不能很好地運(yùn)行的問(wèn)題,后面是拆分成多個(gè)濾波器組合后才解決。今天了解到定點(diǎn)數(shù)字計(jì)算的精度還能超越浮點(diǎn)時(shí),后面應(yīng)付這類問(wèn)題就多了一個(gè)方法。
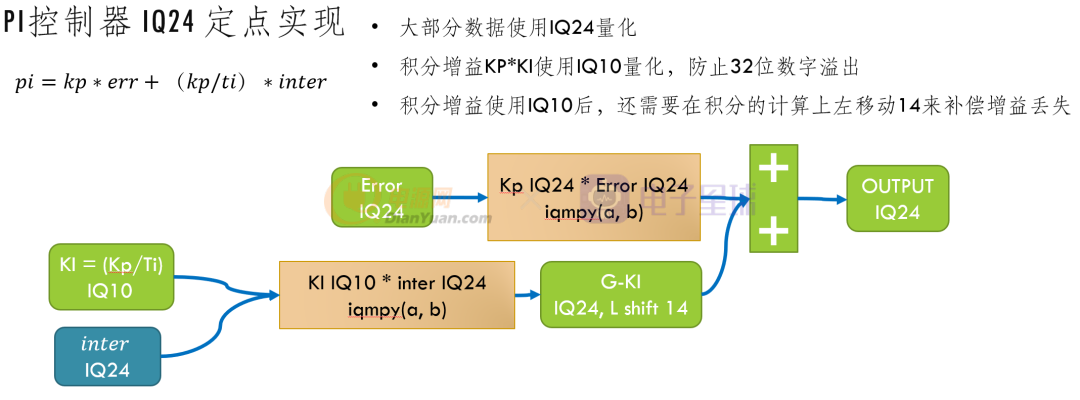
下面嘗試使用一個(gè)PI的定點(diǎn)實(shí)現(xiàn)方法來(lái)學(xué)習(xí)定點(diǎn)編程

實(shí)現(xiàn):
typedef struct PIF_CTRL_LAW_DATA_IQ_TAG{
Uint16 coeff_init_flag;
_iq error_1;
_iq Integrator_output_1;
_iq Integrator_output;
_iq Integrator_gain;
_iq ts;
_iq kp;
_iq ki; /* 1/ti */
_iq pi_out;
_iq output;
_iq max_out;
_iq min_out;
Uint16 integrator_sign;
// LPF
_iq lpf_a_coeff;
_iq _1_lpf_a_coeff;
_iq lpf_out_last;
_iq lpf_out;
}PIF_CTRL_IQ_DATA_DEF;
static inline _iq piF_IQ_func( _iq error,
PIF_CTRL_IQ_DATA_DEF *p,
float32 kp,
float32 ti,
float32 lpc_fc,
float32 ts,
float32 max,
float32 min)
{
if(1u == p->coeff_init_flag) //判斷控制系統(tǒng)初始化
{
if(p->integrator_sign) //抗飽和積分,當(dāng)輸出飽和時(shí)停止累積誤差
{
p->Integrator_output = (_IQmpy(p->ts, (error + p->error_1))) + p->Integrator_output_1;
}
else
{
p->Integrator_output = p->Integrator_output_1;
}
//更新參數(shù)
p->Integrator_output_1 = p->Integrator_output;
p->error_1 = error;
p->Integrator_gain = (_IQ10mpy(p->ki, p->Integrator_output)); //在積分增益初始時(shí)只左移了10位,這里進(jìn)行IQ10*IQ24后,為了達(dá)到IQ24的精度,其實(shí)還需要左移14位,但是兩個(gè)IQ24計(jì)算完成后最要右移24位,所以左移14-右移24,那就是只需要右移10即可完成計(jì)算
p->output = _IQmpy(p->kp, error) + p->Integrator_gain;
p->pi_out = p->output;
//限制幅度
if(p->pi_out > p->max_out) {p->pi_out = p->max_out;}
if(p->pi_out < p->min_out) {p->pi_out = p->min_out;}
//飽和判斷
p->integrator_sign = (p->pi_out == p->output)? 1u : 0u;
// LPF
p->lpf_out = _IQmpy(p->_1_lpf_a_coeff, p->lpf_out_last) + _IQmpy(p->lpf_a_coeff, p->pi_out);
p->lpf_out_last = p->lpf_out;
}
else
{
p->error_1 = 0;
p->Integrator_output = 0;
p->Integrator_output_1 = 0;
p->Integrator_gain = 0;
p->integrator_sign = 1u;
p->output = 0;
p->pi_out = 0;
p->max_out = _IQ(max);
p->min_out = _IQ(min);
//初始化參數(shù)
p->ts = _IQ(ts * 0.5f);
p->kp = _IQ(kp);
//由于積分增益可能很大,為了在32位數(shù)字量化不溢出,僅使用IQ10來(lái)進(jìn)行轉(zhuǎn)換,可以接受丟失精度
p->ki = _IQ10(kp/ti); // L SHIFT 10BIT
p->lpf_out = 0;
p->lpf_out_last = 0;
//低通濾波器參數(shù)計(jì)算
float32 lpf_rc_tao = 1.0f / (lpc_fc * 2.0f * M_PI);
/* 1ORDER LPF a = Ts/(Ts + 1/(2*pi*fc)) */
float32 lpf_a_coeff_f = ts / (ts + lpf_rc_tao);
float32 _1_lpf_a_coeff_f = 1.0f - lpf_a_coeff_f;
p->lpf_a_coeff = _IQ(lpf_a_coeff_f);
p->_1_lpf_a_coeff = _IQ(_1_lpf_a_coeff_f);
p->coeff_init_flag = 1u;
}
return(p->lpf_out);
}本人能力有限,研究定點(diǎn)也才剛開始,如有錯(cuò)誤懇請(qǐng)幫忙指正,謝謝。


